声明: 本文由DataScience原创发表, 转载请注明本文链接mlln.cn, 并在文后留言转载.
本文代码运行环境:
- windows10
- python3.6
- jupyter notebook
- tensorflow 1.x
概述
我们将实现端到端记忆网络(Memory networks), 这个网络的论文在这里。我们将使用Dom Lun的一些辅助函数, 看一下这些函数有助于你对我这篇文章的理解。我们这篇文章专注于实现最简单的记忆网络。在这个过程中,我们将学习如何操纵记忆以获得输出。我们将使用Tensorflow 1.x代码,并偶尔使用Hafner博客的代码。这个博客的最终代码在这里。
我们遵循论文中的任务: 给你一个故事, 你需要找到最终的问题的答案。



论文的的最终目的是找到一种神经网络算法能够根据故事和问题, 找到问题的答案, 在这篇论文中, 答案就是一个单词
什么是记忆网络?
传统上,循环神经网络及其变体(LSTM,GRU)在句子标注和其他自然语言处理任务中非常成功。但是在推理任务方面失败了,他们必须以某种方式记住项目,因为他们缺少“记忆”组件。因此,记忆网络(MN)为这些任务提供了显式记忆,以克服对长期依赖性的限制。他们还使用soft attention来进一步模拟这些记忆的读写。首先,我们将这个特定的记忆网络缩写为MemN2N。这个网络的原始版本是使用matlab实现的, 并且只有1 hop。
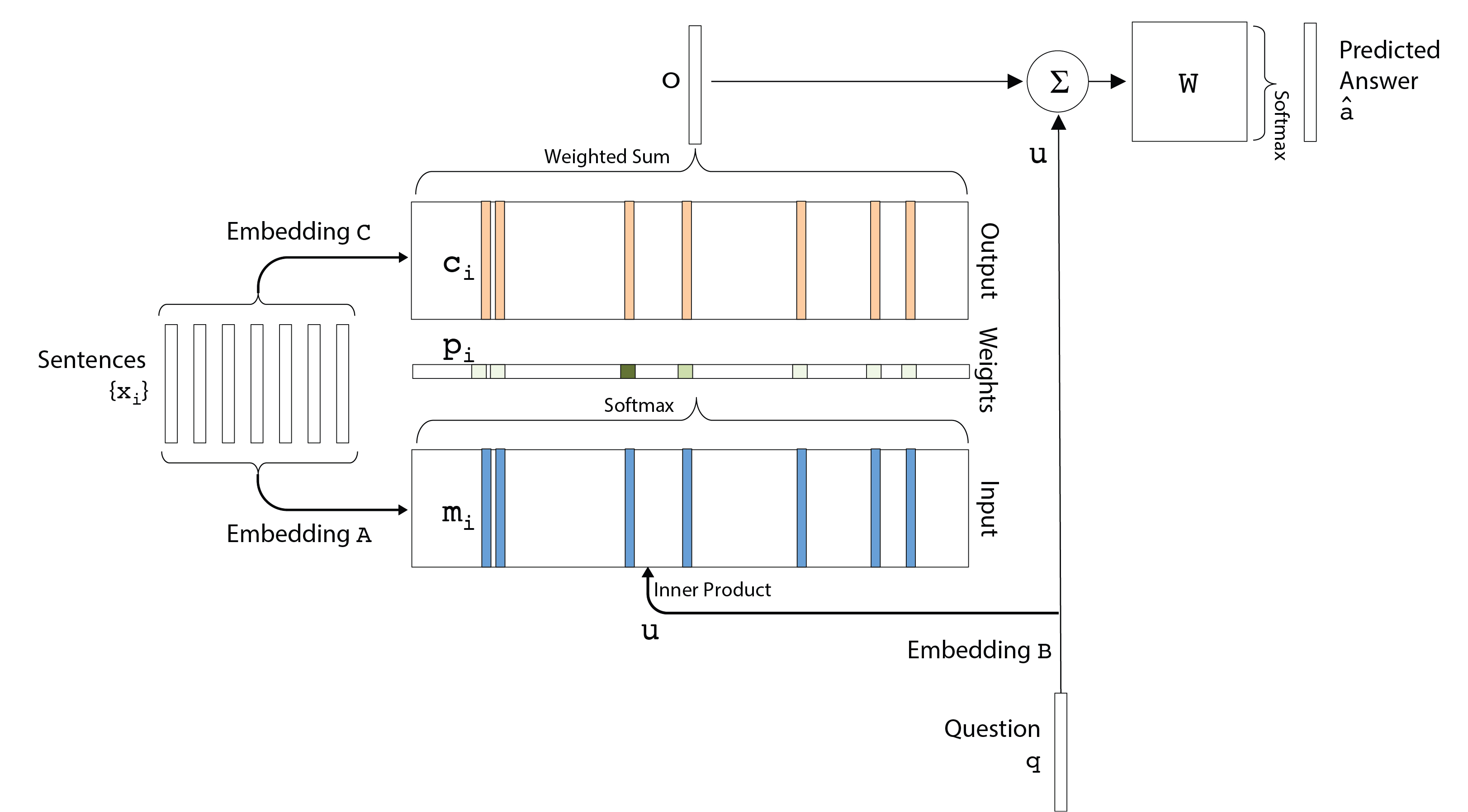
图1
我们将专注于在没有时间编码的情况下复制论文中的bAbI任务。这留给读者练习。现在让我们看一般的MemN2N并逐个编写代码。
拆解记忆网络(MemN2N)
与早期的记忆网络中使用的硬注意力相反,MemN2N使用软注意来选择记忆。这是使用简单的softmax函数完成的。
输入
(仔细观察图1你才能理解下面的话)
我们使用不同的嵌入矩阵向量化所有句子($x_i$),问题($q$)和答案($a$)。因此,我们保留了我们在数据集中看到的所有单词的字典$ V $。字典可以将每个单词都映射到一个索引(数字)。输入包括嵌入矩阵C,A和B.其中C和A分别映射到记忆向量($m_i$)和输出向量($c_i$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| def _create_placeholders(self):
self._lr = tf.placeholder(tf.float32, [], name="learning_rate")
self._stories = tf.placeholder(tf.int32, [None, self._memory_size, self._sentence_size], name="stories")
self._queries = tf.placeholder(tf.int32, [None, self._sentence_size], name="queries")
self._answers = tf.placeholder(tf.int32, [None, self._vocab_size], name="answers")
nil_word = tf.zeros([1, self._embedding_size])
A_placeholder = tf.concat(axis=0, values=
[nil_word, self._normal_init([self._vocab_size-1, self._embedding_size])])
C_placeholder = tf.concat(axis=0, values=
[nil_word, self._normal_init([self._vocab_size-1, self._embedding_size])])
with tf.variable_scope("memn2n"):
self.A_1 = tf.Variable(A_placeholder, name="A")
self.C = []
for hop_number in range(self._hops):
with tf.variable_scope("hop_number{}".format(hop_number)):
self.C.append(tf.Variable(C_placeholder, name="C"))
|
默认情况下,我们将hop数保持为k = 3,如论文中所报告的,这样可以有良好的结果, 并且每个hop共享权重。这就是论文的图示:
 图 2
图 2
记忆(Memory)
在我们继续编写词嵌入部分之前,在论文的第4.1节描述了位置编码算法,以便让句子向量中保存词序信息。如果你不懂位置编码这个算法, 可以看我之前写过的文章: 作文自动评分-位置编码position-encoding(PE)解释。保持最后一个单词独立,因为它表示句子的结束。 作者用Matlab代码定义了这个函数,我们将它转换为python函数。
1
2
3
4
5
6
7
8
9
| def position_encoder(embedding_size, sentence_size):
encoding = np.ones((embedding_size, sentence_size), dtype=np.float32)
for k in range(1, embedding_size+1):
for j in range(1, sentence_size+1):
encoding[k-1, j-1] = (1 - j/sentence_size) - (k/embedding_size) * (1 - 2 * j/sentence_size)
encoding[:, -1] = 1.0
return np.transpose(encoding)
|
我们现在可以添加词索引到词向量再到句子向量转换的代码,tensorflow提供了从句子(词索引的序列)到其向量表示的转换功能。由于这是构建实际网络的部分,因此我们创建了一个新的_inference函数。在这里,我们制作$B$矩阵,它使用与$A$矩阵相同的矩阵来查找单词。因此,同一组权重用于问题和句子。回到图1,我们看到经过$B$给出了结果向量$u$
1
2
3
4
5
6
7
8
9
10
| def _inference(self):
with tf.variable_scope("memn2n"):
B = tf.nn.embedding_lookup(self.A_1, self._queries)
u_1 = tf.reduce_sum(B * self._encoding, 1)
u = [u_1]
|
现在要获得$p_i$,我们必须得到$m_i$并在softmax操作中使用它。它是记忆$m_i$
让我们从其对应的查找中获取mi。我们在每一跳都这样做,这就是第一跳的样子,
(下面的代码紧接上面)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| for hop_number in range(self._hops):
if hop_number == 0:
A_lookup = tf.nn.embedding_lookup(self.A_1, self._stories)
m_A = tf.reduce_sum(A_lookup * self._encoding, 1)
else:
with tf.variable_scope("hop_number{}".format(hop_number-1)):
A_lookup = tf.nn.embedding_lookup(self.C[hop_number-1], self._stories)
m_A = tf.reduce_sum(A_lookup * self._encoding, 1)
u_temp = tf.transpose(tf.expand_dims(u[-1], -1), [0, 2, 1])
dot = tf.reduce_sum(m_A * u_temp, 2)
print(dot.get_shape())
prob = tf.nn.softmax(dot)
P = tf.transpose(tf.expand_dims(prob, -1), [0, 2, 1])
with tf.variable_scope("hop_number{}".format(hop_number)):
C_lookup = tf.nn.embedding_lookup(self.C[hop_number], self._stories)
m_C = tf.reduce_sum(C_lookup * self._encoding, 1)
|
输出
计算得到$P$
1
2
3
4
5
6
| m_C_temp = tf.transpose(m_C, [0, 2, 1])
o_k = tf.reduce_sum(m_C_temp * P, 2)
u_k = u[-1] + o_k
u.append(u_k)
|
得到答案
答案$\hat a$的计算公式是:
$$ \hat{a} = Softmax(W(o + u)) \tag{3} $$
1
2
3
4
|
with tf.variable_scope("hop_number{}".format(hop_number)):
self._logits = tf.matmul(u_k, tf.transpose(self.C[-1], [1,0]))
self._scores = tf.nn.softmax(self._logits)
|
小结
文章到此就是完成了一个端到端的记忆网络, 但是这里还没有介绍如何训练这个网络以及一些可视化的方法。我们统一放在下一篇介绍, 链接:
注意
本文由jupyter notebook转换而来, 您可以在这里下载[notebook](Tensorflow逐步实现记忆网络(Memory networks)第一部分.ipynb)
统计咨询请加QQ 2726725926, 微信 mllncn, SPSS统计咨询是收费的
微博上@mlln-cn可以向我免费题问
请记住我的网址: mlln.cn 或者 jupyter.cn







